La Conquête du Mètre
Pourquoi faire simple quand on peut faire impérial ?
Introduction : Le danger de l’imprécision
Imagine la scène. C’est le 10 août 1628, dans le port de Stockholm. Une foule immense s’est massée sur les quais pour assister à un événement historique : le lancement du Vasa, le navire de guerre le plus puissant et le plus somptueux jamais construit par la Suède. Ce vaisseau de 69 mètres de long, bardé de 64 canons, est un véritable monstre des mers, une démonstration de la puissance du royaume scandinave. Le roi Gustave II Adolphe en personne a supervisé sa construction, exigeant que chaque détail soit parfait. Les canons tonnent en salutation, les voiles se déploient majestueusement, et le Vasa quitte son quai sous les acclamations. Puis, après seulement 1300 mètres de navigation, l’impensable se produit : le navire se met à gîter dangereusement, une rafale de vent le fait chavirer, et en quelques minutes, le fleuron de la marine suédoise sombre dans les eaux du port, emportant avec lui une trentaine de marins. Le Vasa, ce symbole de puissance absolue, n’aura navigué que quelques centaines de mètres avant de devenir un tombeau sous-marin.


Quand les archéologues ont renfloué l’épave en 1961, après 333 ans passés au fond de l’eau, ils ont découvert un navire dans un état de conservation exceptionnel. Mais ils ont aussi mis au jour un mystère qui hante encore les historiens aujourd’hui. Une hypothèse controversée, souvent citée mais toujours débattue, suggère que le naufrage pourrait être dû à une erreur de mesure des plus banales : sur le chantier naval, les charpentiers auraient utilisé deux règles différentes pour construire le navire. D’un côté, le pied suédois standard de 12 pouces, de l’autre, le pied d’Amsterdam de 11 pouces, rapporté par des ouvriers hollandais. Cette différence d’un pouce, répétée sur toute la longueur du navire, aurait créé une asymétrie fatale, rendant le Vasa instable dès sa mise à l’eau. Cette théorie reste discutée parmi les spécialistes, certains pointant plutôt vers des erreurs de conception ou de chargement, mais elle illustre parfaitement un problème qui a hanté l’humanité pendant des millénaires : l’absence d’un système de mesure universel peut être mortelle.
Avant les Lumières, le monde est une véritable tour de Babel des unités. Chaque région, chaque ville, parfois chaque corporation possède ses propres mesures, créant un chaos qui rend le commerce difficile et transforme chaque projet d’ingénierie en pari risqué. L’imprécision des mesures, c’est l’ennemi invisible qui ronge les fondations de la civilisation.
Chapitre 1 : Le Chaos Français : « Deux poids, deux mesures »
Pour comprendre pourquoi la France révolutionnaire va se lancer dans cette folle aventure du système métrique, il faut d’abord saisir l’ampleur du chaos qui règne dans le royaume à la veille de 1789. Imagine un pays où chaque ville, chaque seigneurie, chaque corporation possède ses propres unités de mesure, où un commerçant qui voyage de Paris à Lyon doit littéralement apprendre une nouvelle langue de mesures à chaque étape, où les transactions commerciales ressemblent à des négociations diplomatiques complexes. La France pré-révolutionnaire est un enfer administratif, un cauchemar bureaucratique qui défie l’entendement. Les historiens estiment qu’on y compte plus de 800 noms de mesures différents et près de 250 000 étalons officiels, chacun légèrement différent de son voisin. La pinte de Saint-Denis est significativement plus grosse que la pinte de Paris, le pied de Lyon n’a rien à voir avec le pied de Marseille, et un même mot peut désigner des quantités radicalement différentes selon l’endroit où tu te trouves. Un « boisseau » à Paris ne contient pas la même quantité qu’un « boisseau » à Bordeaux, une « livre » à Toulouse pèse différemment d’une « livre » à Strasbourg, et même les mesures de temps varient d’une région à l’autre. C’est un système qui favorise la confusion, rendant le commerce difficile et servant les intérêts de ceux qui détiennent le pouvoir.

Car derrière ce chaos apparent se cache une logique perverse : les mesures sont un outil d’oppression. Les seigneurs féodaux, qui possèdent le droit de fixer les étalons de mesure sur leurs terres, manipulent savamment ces unités pour prélever plus d’impôts sur les récoltes de leurs paysans. Quand un paysan apporte son grain au moulin seigneurial, le seigneur utilise un boisseau plus grand pour mesurer ce qu’il doit, mais quand il rend la farine, il utilise un boisseau plus petit. Le paysan se retrouve ainsi spolié à chaque transaction, sans même comprendre exactement comment, noyé dans un système de mesures incompréhensible. Cette injustice est si répandue qu’elle donne naissance à une expression qui traverse les siècles : « deux poids, deux mesures ». Cette formule, qui désigne aujourd’hui une inégalité de traitement, trouve son origine dans cette pratique féodale où les seigneurs utilisaient littéralement deux systèmes de mesure différents selon que ça les arrangeait ou non. C’est une arme de domination économique et sociale, un moyen de maintenir les paysans dans la dépendance et l’ignorance, de s’assurer qu’ils ne peuvent jamais vraiment savoir combien ils doivent ou combien on leur doit. Le chaos des mesures, ce n’est pas un accident de l’histoire, c’est un système délibéré de contrôle social.
Face à cette injustice systémique, le peuple français commence à se révolter bien avant 1789. Dans les cahiers de doléances rédigés en prévision des États généraux, une revendication revient avec une régularité obsédante : l’unification des poids et mesures. Les paysans, les artisans, les commerçants, tous demandent la même chose : un seul poids et une seule mesure pour tout le royaume. Cette demande n’est pas anecdotique, elle est centrale dans les aspirations révolutionnaires. Les Français en ont assez de se faire voler par des systèmes de mesure incompréhensibles, assez de devoir jongler avec des dizaines d’unités différentes, assez de voir leurs récoltes confisquées par des seigneurs qui manipulent les étalons à leur avantage. Ils veulent la transparence, l’égalité, la justice. Et cette revendication va trouver un écho puissant dans l’esprit des révolutionnaires, qui voient dans l’unification des mesures un moyen de briser définitivement l’ancien système féodal, de créer une France unifiée et égalitaire, où tous les citoyens sont soumis aux mêmes règles, aux mêmes mesures, aux mêmes lois.
Il faudra une Révolution pour tenter de régler ce chaos millénaire. Pas juste une révolution politique, mais une révolution scientifique, philosophique et culturelle qui va bouleverser notre rapport au monde. La France de 1789, en pleine effervescence révolutionnaire, va se lancer dans une aventure folle : créer un système de mesure universel, « pour tous les hommes, pour tous les temps », basé non plus sur l’arbitraire humain mais sur les constantes immuables de la nature. Cette épopée va donner naissance au système métrique, cette invention géniale que nous utilisons aujourd’hui sans même y penser. Mais la bataille sera rude, semée d’obstacles politiques, de résistances populaires, et de tragédies historiques. Et surtout, cette histoire n’est pas terminée : trois siècles après la création du mètre, une superpuissance mondiale continue de résister à cette évidence, préférant payer le prix de l’imprécision plutôt que d’abandonner ses vieilles habitudes. L’histoire du système métrique, ce n’est pas une histoire de mathématiques poussiéreuses, c’est une bataille épique contre l’habitude humaine et le hasard, dont les conséquences se font encore sentir aujourd’hui, parfois de la façon la plus dramatique qui soit.
Chapitre 2 : L’Épopée Scientifique : Le « Système Divin »
L’idée qui va donner naissance au système métrique est d’une simplicité géniale, mais aussi d’une ambition folle : créer une mesure universelle, « pour tous les hommes, pour tous les temps ». Les savants des Lumières, emmenés par des figures comme Condorcet et Laplace, comprennent que pour échapper au chaos des mesures locales, il faut abandonner toute référence à l’humain. Plus de pieds, plus de pouces, plus de coudées basées sur la taille d’un roi ou d’un seigneur. Ces mesures changent, varient, sont arbitraires. Il faut trouver une référence absolue, immuable, universelle. Et cette référence, les savants la trouvent dans la Terre elle-même. La planète est éternelle, elle est la même partout, elle appartient à tous les hommes. Alors pourquoi ne pas baser la mesure fondamentale sur la circonférence de la Terre ? C’est ainsi que naît la définition du mètre : la dix-millionième partie du quart du méridien terrestre. Une définition qui semble abstraite, mais qui cache une ambition scientifique et philosophique colossale. Il ne s’agit plus de mesurer avec des étalons locaux, mais de mesurer la Terre elle-même pour créer l’étalon universel. C’est une révolution copernicienne appliquée aux mesures : l’homme n’est plus au centre, c’est la planète qui devient la référence absolue.

Mais définir le mètre, c’est une chose. Le mesurer, c’en est une autre. Pour connaître la longueur exacte du quart du méridien terrestre, il faut mesurer un arc de méridien avec une précision jamais atteinte auparavant. L’Assemblée nationale, en 1791, confie cette mission titanesque à deux astronomes de génie : Jean-Baptiste Delambre et Pierre-François Méchain. Leur mission : mesurer la distance entre Dunkerque et Barcelone, deux villes situées approximativement sur le même méridien, en utilisant la technique de la triangulation géodésique. Cette méthode consiste à créer une chaîne de triangles qui s’étend sur toute la distance, en mesurant les angles avec des instruments de précision et en calculant les distances par trigonométrie. C’est un travail de fourmi, qui nécessite de monter sur des clochers, des montagnes, des tours, pour établir des points de mesure parfaitement alignés. Delambre part de Dunkerque et descend vers le sud, Méchain part de Barcelone et remonte vers le nord, ils doivent se rencontrer quelque part au milieu. Leur mission est prévue pour durer quelques mois. Elle va finalement durer sept ans, de 1792 à 1799, et devenir une véritable épopée digne d’un roman d’aventure.
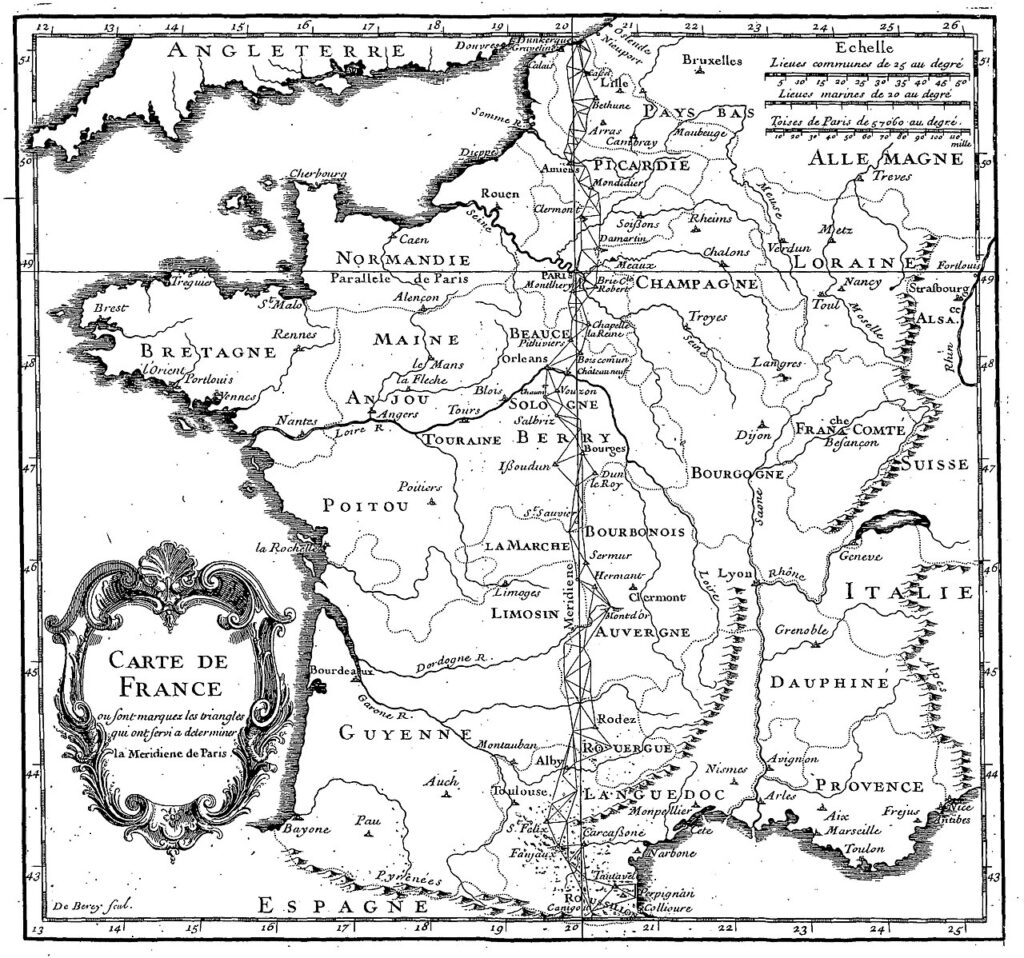
Car les deux savants partent en mission au pire moment possible : la France est en pleine Révolution, et bientôt la Terreur va s’abattre sur le pays. Delambre et Méchain, avec leurs instruments étranges, leurs calculs mystérieux, leurs observations du ciel, sont rapidement suspectés d’être des espions. À chaque village, à chaque étape, ils doivent expliquer leur mission, montrer leurs papiers, convaincre les autorités locales qu’ils ne sont pas des agents de l’étranger. Delambre se fait arrêter plusieurs fois, ses instruments sont confisqués, il doit faire appel à des lettres de recommandation de savants parisiens pour être libéré. Méchain, de son côté, tombe gravement malade, est bloqué en Espagne par la guerre, et vit dans l’angoisse constante d’être pris pour un espion. Les deux hommes travaillent dans des conditions épouvantables : ils doivent monter sur des clochers en ruine, installer leurs instruments par tous les temps, faire des observations astronomiques de nuit, calculer pendant des heures à la lueur d’une bougie. C’est « Indiana Jones avec des règles à calcul », une aventure scientifique où chaque mesure est une victoire, où chaque triangle calculé est un pas de plus vers la définition du mètre. Et malgré tous ces obstacles, malgré la guerre, la maladie, les arrestations, les deux savants réussissent leur mission. En 1799, ils présentent leurs résultats à l’Académie des sciences, et le mètre est officiellement défini.
Mais la beauté du système métrique ne s’arrête pas à la définition du mètre. Ce qui rend ce système véritablement génial, c’est sa cohérence absolue, sa logique implacable. Tout découle du mètre par une série de relations mathématiques parfaites. Le volume ? C’est le cube d’un décimètre, ce qui donne exactement un litre. La surface ? C’est le carré d’un décamètre (10 mètres), ce qui donne exactement un are (100 mètres carrés), et avec le préfixe hecto, on obtient l’hectare (100 ares, soit 10 000 mètres carrés), une unité créée pour remplacer les anciennes mesures agraires comme l’arpent. La masse ? C’est le poids d’un litre d’eau pure à la température de 4 degrés Celsius, ce qui donne exactement un kilogramme. La force ? C’est la force nécessaire pour accélérer un kilogramme d’un mètre par seconde au carré, ce qui donne exactement un newton. L’énergie ? C’est la force d’un newton appliquée sur une distance d’un mètre, ce qui donne exactement un joule. Chaque unité est liée à la précédente par une relation mathématique simple et élégante. C’est un système où tout s’emboîte parfaitement, où chaque mesure est définie de façon logique et cohérente. Compare ça au système impérial : une lieue équivaut à 3 miles, un mile à 8 stades, un stade à 10 chaînes, une chaîne à 22 yards, un yard à 3 pieds, un pied à 3 mains, une main à 4 pouces, un pouce à 3 orges, une orge à 333 millièmes de pouces, un millième de pouce à 1,44 TWP, et un TWP à 17,64 microns. Pourquoi 3 ? Pourquoi 8 ? Pourquoi 22 ? Pourquoi 333 ? Pourquoi 1,44 ? Pourquoi 17,64 ? Aucune logique, c’est du pur « par cœur », une cascade de conversions arbitraires héritées de siècles d’histoire chaotique, où chaque nombre semble avoir été choisi au hasard ou selon des critères oubliés depuis longtemps. Un gallon équivaut à 231 pouces cubes, ce qui équivaut à 8,34 livres. Pourquoi 231 ? Pourquoi 8,34 ? Personne ne le sait vraiment, c’est comme ça et c’est tout. Le système métrique, lui, est une œuvre d’art mathématique, un système où chaque nombre a un sens, où chaque unité est là pour une raison précise, où tout s’emboîte avec une élégance qui fait pleurer de joie les mathématiciens. C’est cette beauté logique qui va finir par conquérir le monde, ou presque.
Chapitre 3 : La Bataille des Mots : Politique et Étymologie
Créer un système de mesure universel, c’est bien. Mais lui donner un nom, c’est une autre affaire, et ça peut devenir un champ de bataille politique et linguistique. Les révolutionnaires français comprennent très vite que les mots ont un pouvoir immense, que le nom qu’on donne aux choses influence la façon dont on les perçoit. Alors quand il s’agit de nommer la nouvelle unité de mesure fondamentale, le choix n’est pas anodin. Les savants optent pour « mètre », un mot qui vient du grec « metron », qui signifie simplement « mesure ». Mais ce n’est pas juste un choix étymologique innocent. « Metron » en grec, c’est aussi ce qui mesure, ce qui juge, ce qui établit la norme. En choisissant ce nom, les révolutionnaires envoient un message clair : cette unité n’est pas une mesure parmi d’autres, c’est LA mesure, la référence absolue, la norme universelle. C’est un nom choisi pour s’imposer, pour écraser les anciennes unités, pour dire « tout le reste est obsolète, c’est moi la vraie mesure ». C’est de la politique linguistique pure, une façon de faire passer un message révolutionnaire à travers l’étymologie. Le mètre, ce n’est pas juste une unité de longueur, c’est un manifeste politique et scientifique en un seul mot.
Mais le système métrique ne se contente pas d’une seule unité, il faut aussi créer des multiples et des sous-multiples pour couvrir toutes les échelles de mesure. Et là encore, les révolutionnaires font un choix linguistique délibéré et brillant : ils utilisent des préfixes grecs pour les multiples et des préfixes latins pour les sous-multiples. Pour multiplier l’unité, on a donc déca (du grec « deka », dix), hecto (du grec « hekaton », cent), kilo (du grec « khilioi », mille), et plus tard méga, giga, téra. Pour diviser l’unité, on a déci (du latin « decimus », dixième), centi (du latin « centesimus », centième), milli (du latin « millesimus », millième), et plus tard micro, nano, pico. Cette distinction n’est pas anodine : elle crée une cohérence linguistique parfaite, où chaque préfixe raconte son histoire étymologique. Quand tu dis « kilomètre », tu sais immédiatement que c’est un multiple (grec), et quand tu dis « centimètre », tu sais que c’est un sous-multiple (latin). C’est une façon élégante de structurer le langage scientifique, de créer des règles claires et mémorisables. Cette logique initiale ne sera pas toujours respectée par la suite, avec des exceptions comme « micro » qui est grec mais désigne un sous-multiple, mais l’idée de base reste : le système métrique, même dans ses préfixes, est pensé pour être cohérent, logique, universel.
Mais si le nom du mètre est un succès, celui de l’unité de masse va devenir un véritable scandale qui hante encore le système métrique aujourd’hui. À l’origine, les savants voulaient appeler l’unité de base de masse le « grave », du latin « gravitas », qui signifie la pesanteur, la gravité. C’est un nom logique, élégant, qui fait sens : le grave, c’est ce qui pèse, ce qui a du poids. Mais voilà, nous sommes en pleine Terreur révolutionnaire, et le mot « grave » sonne trop proche de « gras », qui évoque les nobles, les riches, les oppresseurs. Dans la folie paranoïaque de l’époque, où chaque mot peut être suspect, où chaque référence à l’ancien régime est traquée, le « grave » est rejeté. Les révolutionnaires le remplacent par le « gramme », un mot minuscule, presque insignifiant, qui ne fait référence à rien de politique. Mais cette décision va créer une aberration qui perdure encore aujourd’hui : le gramme est si petit qu’il est inutilisable dans la vie quotidienne. Alors on est obligé d’utiliser le « kilogramme », avec son préfixe « kilo », comme unité de base. C’est absurde : l’unité de base du système métrique, celle qu’on utilise partout, s’appelle « kilogramme », ce qui signifie littéralement « mille grammes ». C’est comme si on appelait le mètre le « kilomillimètre ». Cette aberration, héritée de la paranoïa révolutionnaire, continue de compliquer la vie des scientifiques et des étudiants du monde entier, qui doivent se rappeler que l’unité de base de la masse, c’est le kilogramme, pas le gramme.
Pour le volume, les révolutionnaires vont utiliser une astuce marketing bien plus subtile. Ils créent une nouvelle unité, le « litre », qui correspond exactement au volume d’un décimètre cube. Mais au lieu de choisir un nom complètement nouveau, ils reprennent le nom du « litron », une ancienne unité de mesure française qui désignait une bouteille de vin. C’est une manœuvre politique brillante : en réutilisant un nom familier, les révolutionnaires rassurent le peuple, lui donnent l’impression que le nouveau système n’est pas si différent de l’ancien. Le litron, c’est ce que tout le monde connaît, c’est ce qu’on utilise au marché, c’est ce qu’on boit au cabaret. En le transformant en « litre », on garde la familiarité tout en changeant la définition. C’est de la manipulation linguistique douce, une façon de faire passer la pilule révolutionnaire en la sucrant avec un nom rassurant. Le peuple français, qui déteste déjà le système métrique abstrait, va au moins reconnaître ce mot-là, ce qui va faciliter l’adoption du litre, même si le reste du système reste incompréhensible. Cette stratégie montre que les révolutionnaires comprennent parfaitement que changer les mesures, c’est aussi changer les mots, et que changer les mots, c’est changer la façon dont les gens pensent. La bataille du système métrique ne se joue pas seulement dans les laboratoires et sur les chantiers, elle se joue aussi dans les dictionnaires et dans les têtes des gens.
Chapitre 4 : La Résistance Française : Le Mètre détesté
Malgré toute la logique scientifique et la beauté mathématique du système métrique, malgré les efforts des révolutionnaires pour le rendre accessible et familier, le peuple français le déteste. Dès son adoption officielle en 1795, la résistance s’organise. Les Français, qui ont réclamé l’unification des mesures dans leurs cahiers de doléances, se retrouvent face à un système qu’ils ne comprennent pas, qu’ils trouvent abstrait, déconnecté de leur réalité quotidienne. Le mètre, c’est quoi ? La dix-millionième partie du quart du méridien terrestre ? Ça ne veut rien dire pour un paysan qui veut mesurer son champ, pour un boulanger qui veut peser sa farine, pour un marchand qui veut vendre ses légumes. Les anciennes mesures, elles, avaient du sens : un pied, c’est la longueur d’un pied, une livre, c’est ce qu’on peut soulever facilement, une pinte, c’est ce qu’on boit dans un verre. Le système métrique, lui, est trop abstrait, trop scientifique, trop éloigné de la vie de tous les jours. Alors les Français résistent. Ils cachent leurs vieilles règles sous le manteau, continuent à utiliser les anciennes unités en secret, refusent d’apprendre les nouvelles mesures. Les marchés continuent à fonctionner avec les anciennes unités, les artisans refusent de changer leurs outils, les paysans continuent à mesurer leurs champs en arpents et leurs récoltes en boisseaux. Le système métrique est officiel, mais dans la pratique, il est largement ignoré. C’est un échec retentissant, une révolution scientifique qui se heurte à la force de l’habitude et à la résistance du quotidien.
Face à cette résistance massive, Napoléon Bonaparte, qui a pris le pouvoir en 1799, comprend qu’il faut faire un compromis. Lui-même, selon les témoignages de l’époque, critique le système métrique qu’il juge trop abstrait et difficile à comprendre pour le peuple. En 1812, il prend une décision qui va marquer l’histoire du système métrique : il autorise les « mesures usuelles », un système hybride qui mélange les anciennes unités et les nouvelles. Les mesures usuelles, c’est un compromis politique brillant : on garde les noms familiers (pied, livre, pinte), mais on les redéfinit en fonction du système métrique. Un pied usuel équivaut à un tiers de mètre, une livre usuelle à 500 grammes, une pinte usuelle à un litre. C’est une façon de faire la transition en douceur, de ne pas brusquer les habitudes, de donner au peuple l’impression qu’on garde ce qu’il connaît tout en modernisant le système. Mais cette décision va créer un chaos encore plus grand : la France vit désormais dans un système hybride, où les anciennes mesures coexistent avec les nouvelles, où personne ne sait vraiment quelle unité utiliser, où les conversions deviennent un cauchemar. Pendant trente ans, de 1812 à 1842, la France navigue dans ce système schizophrène, où les scientifiques utilisent le système métrique pur, les commerçants utilisent les mesures usuelles, et les paysans continuent à utiliser les anciennes unités. C’est un retour en arrière, un aveu d’échec, une preuve que changer les habitudes est plus difficile que changer les lois.
Il faudra attendre 1837, sous le règne de Louis-Philippe, pour que le système métrique redevienne obligatoire. La loi du 4 juillet 1837 impose le système métrique dans toute la France, interdit l’usage des anciennes unités sous peine d’amende, et met fin définitivement aux mesures usuelles. Cette fois, l’État ne transige plus : le système métrique est la seule mesure légale, point final. Les vieilles règles sont confisquées, les étalons anciens sont détruits, les commerçants qui continuent à utiliser les anciennes unités sont sanctionnés. C’est une victoire tardive, acquise après des décennies de résistance, mais c’est une victoire définitive. Le système métrique finit par s’imposer, non pas parce que les Français l’aiment, mais parce qu’ils n’ont plus le choix. L’habitude finit par l’emporter, la force de la loi finit par vaincre la résistance populaire. Et petit à petit, les Français s’habituent au mètre, au kilogramme, au litre. Ils apprennent à penser en décimètres plutôt qu’en pieds, en grammes plutôt qu’en onces, en litres plutôt qu’en pintes. Le système métrique devient naturel, évident, universel. Mais cette victoire a été longue, difficile, semée d’obstacles et de résistances. Et surtout, cette histoire montre que même le système le plus logique, le plus scientifique, le plus universel, peut échouer s’il ne prend pas en compte la force de l’habitude humaine.
Chapitre 5 : L’Amérique à contre-courant : L’Histoire bégaye
Pendant que la France révolutionnaire se débat avec son nouveau système métrique, de l’autre côté de l’Atlantique, les États-Unis d’Amérique, fraîchement indépendants, regardent cette innovation avec intérêt. Thomas Jefferson, alors secrétaire d’État et futur président, est un francophile convaincu, un admirateur des Lumières françaises, et il voit dans le système métrique une opportunité historique. Les États-Unis, qui viennent de se libérer de la tutelle britannique, cherchent à se démarquer de l’ancien monde, à créer leur propre identité. Adopter le système métrique dès sa création, ce serait un geste symbolique fort : rejeter les unités impériales britanniques, s’allier avec la France révolutionnaire, embrasser la modernité scientifique. Jefferson attend donc avec impatience les étalons métriques que la France doit lui envoyer, ces prototypes officiels qui permettront aux États-Unis d’adopter le système métrique dès son invention. C’est une occasion unique, un moment historique où l’Amérique pourrait devenir le premier pays à adopter le système métrique en dehors de la France, où elle pourrait montrer au monde qu’elle est une nation moderne, scientifique, progressiste.
Mais l’histoire en décide autrement. En 1793, la France envoie le scientifique Joseph Dombey vers les États-Unis avec les précieux étalons métriques. Dombey embarque sur un navire français, chargé de cette mission diplomatique et scientifique cruciale. Mais la traversée de l’Atlantique est dangereuse, surtout en pleine guerre entre la France et la Grande-Bretagne. Le navire de Dombey est intercepté par des corsaires britanniques, ces pirates légaux qui écument les mers au nom de la couronne. Dombey est capturé, ses étalons sont confisqués ou perdus, et le scientifique français meurt en captivité à Montserrat en 1794, sans jamais avoir atteint les côtes américaines. Cette tragédie maritime va changer le cours de l’histoire : les États-Unis ne recevront jamais les étalons métriques, Jefferson ne pourra jamais présenter le système métrique au Congrès, et l’Amérique va manquer l’occasion historique d’adopter le système métrique dès son invention. C’est un moment charnière, un de ces « et si » de l’histoire : si Dombey avait réussi sa mission, si les pirates n’avaient pas intercepté son navire, si les étalons étaient arrivés à bon port, peut-être que les États-Unis utiliseraient aujourd’hui le système métrique comme le reste du monde. Mais l’histoire ne se refait pas, et cette occasion manquée va peser lourd sur l’avenir des États-Unis.
Près de deux siècles plus tard, dans les années 1970, le monde entier a adopté le système métrique. Seuls les États-Unis, le Liberia et la Birmanie résistent encore. Les États-Unis, cette superpuissance mondiale, cette nation qui envoie des hommes sur la Lune, qui domine la science et la technologie, continue d’utiliser un système de mesures archaïque hérité de l’ancien empire britannique. C’est un paradoxe absurde : les scientifiques américains travaillent en métrique, la NASA utilise le système métrique, mais l’industrie et la vie quotidienne restent bloquées dans le système impérial. En 1975, le Congrès américain vote le Metric Conversion Act, une loi qui encourage la conversion au système métrique. C’est un geste courageux, une tentative de rattraper le retard historique, de rejoindre enfin le reste du monde. Des panneaux routiers sont changés, des manuels scolaires sont réécrits, des entreprises commencent à convertir leurs processus. Mais la résistance culturelle est massive. Les Américains voient le système métrique comme « antiaméricain », comme une attaque contre leur identité, comme une soumission à l’étranger. Les médias se moquent de cette « invasion métrique », les politiciens populistes dénoncent cette « folie européenne », et le mouvement de conversion s’enlise dans les polémiques et les résistances.
En 1982, l’administration Reagan met fin au financement fédéral de la conversion métrique. C’est un coup d’arrêt brutal, un retour en arrière, un aveu d’échec. Le Metric Conversion Act n’est pas abrogé, mais il devient lettre morte, sans moyens, sans volonté politique, sans soutien populaire. Les États-Unis abandonnent officiellement leur tentative de conversion, préférant rester isolés dans leur système impérial plutôt que de faire l’effort de rejoindre le reste du monde. C’est un choix politique et culturel, mais c’est aussi un choix économique et scientifique qui va coûter cher. Car en refusant le système métrique, les États-Unis se condamnent à vivre dans un monde schizophrène, où la science utilise un système et l’industrie un autre, où les conversions d’unités deviennent un piège permanent, où chaque projet international devient un casse-tête de conversions. Cette résistance obstinée au système métrique, cette fierté mal placée dans l’archaïsme, va finir par coûter très cher aux États-Unis, parfois de la façon la plus dramatique qui soit.
Chapitre 6 : La Facture Salée : Mars Climate Orbiter (1999)
Le 23 septembre 1999, la NASA perd le contact avec Mars Climate Orbiter, une sonde spatiale de 327 millions de dollars qui devait étudier le climat martien.
La sonde, qui devait se placer en orbite autour de Mars, disparaît soudainement, sans explication. Les ingénieurs de la NASA sont perplexes : tous les systèmes semblent avoir fonctionné correctement, la trajectoire était bonne, les communications étaient établies. Mais la sonde a simplement disparu, comme si elle s’était évaporée dans l’espace. L’enquête qui suit va révéler une erreur d’une simplicité désarmante, une erreur qui aurait pu être évitée si les États-Unis utilisaient le système métrique comme le reste du monde. Car le problème, c’est que les États-Unis vivent dans un monde schizophrène : la science utilise le système métrique, mais l’industrie continue d’utiliser le système impérial. Et quand ces deux mondes se rencontrent, ça peut mal tourner.
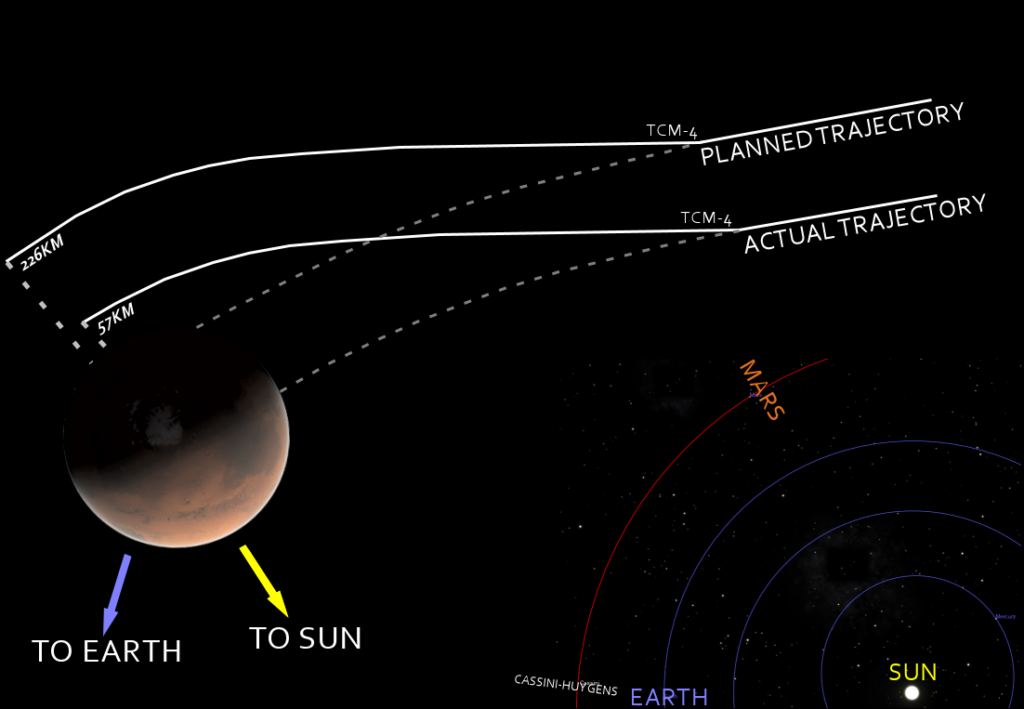
Mars Climate Orbiter est construite par Lockheed Martin, une entreprise privée qui travaille pour la NASA. Lockheed Martin, comme la plupart des entreprises américaines, utilise le système impérial dans ses calculs et ses logiciels. Quand l’entreprise calcule les forces de poussée des moteurs de la sonde, elle utilise des livres-force, l’unité impériale de force. Mais la NASA, elle, travaille en système métrique, et ses logiciels de navigation attendent des données en newtons, l’unité métrique de force. Le problème, c’est qu’une livre-force n’est pas égale à un newton. En fait, une livre-force équivaut à environ 4,45 newtons. Quand Lockheed Martin envoie ses données à la NASA, personne ne vérifie les unités. Les ingénieurs de la NASA reçoivent des valeurs qu’ils pensent être en newtons, mais qui sont en réalité en livres-force. Ils utilisent donc des forces quatre fois et demie plus petites que prévu pour calculer la trajectoire de la sonde. Résultat : la sonde s’approche trop près de Mars, pénètre dans l’atmosphère martienne à une altitude trop basse, et brûle littéralement dans l’atmosphère. Une erreur de conversion d’unités a détruit une mission de 327 millions de dollars, une mission qui avait mis des années à être préparée, une mission qui devait révolutionner notre compréhension du climat martien.
Le rapport d’enquête de la NASA est accablant. Il pointe du doigt cette erreur de conversion d’unités comme cause principale de la perte de la sonde. Mais il révèle aussi quelque chose de plus profond : cette erreur n’est pas un accident isolé, c’est le symptôme d’un problème systémique. Les États-Unis, en refusant d’adopter complètement le système métrique, se condamnent à vivre dans un monde où chaque projet scientifique et industriel devient un casse-tête de conversions. Chaque fois qu’une entreprise privée travaille avec une agence gouvernementale, chaque fois qu’un laboratoire collabore avec l’industrie, il faut vérifier les unités, convertir les données, s’assurer que tout le monde parle la même langue. Et malgré toutes ces précautions, des erreurs se glissent, des conversions sont oubliées, des unités sont mélangées. Mars Climate Orbiter n’est pas un cas isolé. En 1983, le vol Air Canada 143, surnommé le « Gimli Glider », a épuisé son carburant en plein vol à cause d’une confusion entre livres et kilogrammes lors du ravitaillement. L’avion a réussi un atterrissage d’urgence miraculeux, mais l’erreur aurait pu être fatale. En 1999, le vol Korean Air Cargo 6316 s’est écrasé à Shanghai après qu’une confusion entre mètres et pieds ait conduit l’équipage à descendre trop bas, causant la mort de huit personnes. Ces catastrophes illustrent parfaitement ce risque permanent : dans un monde où deux systèmes de mesure coexistent, chaque mission, chaque projet, chaque collaboration devient un piège potentiel. C’est le prix à payer pour cette résistance obstinée au système métrique, cette fierté mal placée dans l’archaïsme.
En 1628, le Vasa sombrait peut-être à cause d’une erreur de mesure, d’une confusion entre deux systèmes de mesure différents. En 1999, 371 ans plus tard, Mars Climate Orbiter brûle dans l’atmosphère martienne à cause d’une erreur de conversion entre deux systèmes de mesure différents. L’histoire se répète, les mêmes erreurs produisent les mêmes catastrophes. L’absence d’un système de mesure universel continue de tuer, de détruire, de faire perdre des fortunes. Le Vasa et Mars Climate Orbiter sont deux échos lointains mais terriblement similaires : deux projets ambitieux détruits par l’imprécision des mesures, deux symboles de la folie humaine qui préfère la tradition à la logique, l’habitude à la raison. Et pendant ce temps, le reste du monde utilise le système métrique, un système où tout s’emboîte parfaitement, où les conversions sont simples, où les erreurs sont rares. Les États-Unis, cette superpuissance qui domine le monde, continue de payer le prix de son archaïsme, parfois de la façon la plus dramatique qui soit.
Conclusion
L’histoire du système métrique est une épopée fascinante, un récit où la science, la politique, la culture et l’habitude humaine s’affrontent dans une bataille qui dure encore aujourd’hui. C’est l’histoire d’une victoire de la raison sur la tradition, mais une victoire acquise dans la douleur, semée d’obstacles, de résistances et de tragédies. Le système métrique, cette invention géniale née de la Révolution française, cette œuvre d’art mathématique où chaque unité s’emboîte parfaitement avec la suivante, a fini par conquérir presque toute la planète. Presque. Car aujourd’hui, le monde est unifié autour d’un système de mesure universel, logique, cohérent. Presque tous les pays utilisent le mètre, le kilogramme, le litre, le newton, le joule. Presque tous, sauf une superpuissance mondiale qui continue de résister, qui préfère payer le prix de l’archaïsme plutôt que de faire l’effort de rejoindre le reste du monde. Les États-Unis, cette nation qui domine la science et la technologie, continue d’utiliser un système de mesures hérité de l’ancien empire britannique, un système où les conversions sont un cauchemar, où les erreurs sont fréquentes, où chaque collaboration internationale devient un piège potentiel.
Et pourtant, cette résistance obstinée n’était peut-être pas inévitable. En 1793, Joseph Dombey embarquait vers les États-Unis avec les précieux étalons métriques, ces prototypes officiels qui auraient permis à l’Amérique d’adopter le système métrique dès son invention. Dombey transportait la solution, il transportait l’avenir, il transportait la possibilité d’un monde unifié autour d’un système de mesure universel. Mais les corsaires britanniques ont intercepté son navire, Dombey est mort en captivité, les étalons ont été perdus, et l’histoire a pris un autre chemin. Si Dombey avait réussi sa mission, si les pirates n’avaient pas intercepté son navire, si les étalons étaient arrivés à bon port, peut-être que les États-Unis utiliseraient aujourd’hui le système métrique comme le reste du monde. Peut-être que Mars Climate Orbiter n’aurait jamais brûlé dans l’atmosphère martienne, peut-être que des vies auraient été épargnées, peut-être que des fortunes n’auraient pas été perdues. Mais l’histoire ne se refait pas, et les pirates ont changé le cours de l’histoire. Aujourd’hui, trois siècles après la création du mètre, l’absence d’un système de mesure universel continue de tuer, de détruire, de faire perdre des fortunes. Et pendant ce temps, le reste du monde utilise le système métrique, cette invention géniale que nous utilisons sans même y penser, cette victoire de la raison sur la tradition, cette preuve que l’humanité peut parfois choisir la logique plutôt que l’habitude, l’universel plutôt que le local, l’avenir plutôt que le passé.